Natural Computing Lecture, February 22, 2022

Cellular automata

Simple models of dynamic interactions in (2D) biological systems

Inge Wortel
inge.wortel@ru.nl
Data Science, RU

Why you should care about biology

Typical problems encountered by computer scientists:

Storing, processing, and transferring information

Efficient data structures to store & access data
Processing data and "learning" patterns from it (machine learning, data science)
Transferring information (e.g. copying, moving)

Optimization

Travelling salesman problem
Fastest way to get from A to B
... etc

Security and anomaly detection

Detect spam, computer viruses
Detect anomalies to spot potential fraud

Why you should care about biology

Typical problems encountered by computer scientists: analogies to the natural world!

Storing, processing, and transferring information

Efficient data structures to store & access data (DNA, immune memory)
Processing data and "learning" patterns from it (processing DNA, "learning" by the brain)
Transferring information (genetics)

Optimization

Darwinian selection

Security and anomaly detection

Immune system detects harmful invaders (bacteria, viruses)

Natural computing: the "bigger picture"

Two basic questions at the heart of this course:

Can we design algorithms for computing science problems that are inspired by the natural world?
(i.e. to solve tasks such as information processing and optimization?)
Can we improve our understanding of the natural world by using computer science algorithms?
("What I cannot create, I do not understand" - Richard Feynman)

Natural computing: the "bigger picture"

Two basic questions at the heart of this course:

Can we design algorithms for computing science problems that are inspired by the natural world?
(i.e. to solve tasks such as information processing and optimization?)
Can we improve our understanding of the natural world by using computer science algorithms?
("What I cannot create, I do not understand" - Richard Feynman)

You already know several examples related to Q1:

(Artificial neural networks: inspired by our "learning organ")
Evolutionary algorithms: inspired by natural selection & genetics
Swarm intelligence: inspired by natural "swarms"

Natural computing: the "bigger picture"

Two basic questions at the heart of this course:

Can we design algorithms for computing science problems that are inspired by the natural world?
(i.e. to solve tasks such as information processing and optimization?)
Can we improve our understanding of the natural world by using computer science algorithms?
("What I cannot create, I do not understand" - Richard Feynman)

Coming weeks: focus on Q2 by modelling biological systems in space and time:

Simple models: CAs (this week)
More complicated: CPMs (next week)

Why model biological systems?

Models can help us to:

predict how a system develops over time
understand the consequences of those developments
change the behaviour of a system.
"debug" our understanding

The ultimate question: what will happen next?

Spatial models of biological systems

Cellular automata

Cellular automata are simple spatial models:

They consist of pixels on a grid
Each pixel can have different states...
... which change over time according to some rules.

Formally, the "grid" is a graph ${\cal G}=(\mathbf{V},\mathbf{E})$ with:

"vertices" $\mathbf{V}$, the pixels on this grid
"edges" $\mathbf{E}$, determinining which pixels count as "adjacent"

We'll use the "Moore neighborhood" where each pixel has edges to its 8 neighbors: N, E, S, W, NE, SE, SW, NW
Boundary conditions: what to do with border pixels where neighbors are unknown? (E.g. "periodic" boundary)

Pixels (vertices) can have different values: the "states"

Cellular automata

Cellular automata are simple spatial models:

They consist of pixels on a grid
Each pixel can have different states...
... which change over time according to some rules.

Example: bacterial colony growth (very simple model):

Grid represents a 2D petridish
Pixels can have two states: with (black) or without (white) bacteria
Rule: any white pixel adjacent to a black pixel becomes black as well.

Discuss
How will the colony in the upper right corner of this slide grow? Is that realistic? Can you think of some way to improve this model?

Cellular automata

The problem with our previous rule:

So how do we fix this?

Rules do not have to be deterministic

You might argue that pixels with more infected (black) neighbors are more likely to become infected, so let's change our rule:
$\rightarrow$ chance of becoming black = # black neighbors x 10%

Definition
We call a model deterministic if the same starting point always leads to the same result. Otherwise, we call it stochastic.
.

Key Point
We can make many different cellular automata by inventing new rules.

Another model: how does infection spread in a population?

The SIR model: individuals can be

Susceptible
(= healthy, but they can still become infected)
Infected
Resistant
(= healthy, and can no longer be infected)

Discuss
How would you convert this model into a cellular automaton? (What should the grid represent? And the states? What rules can you come up with, and are they deterministic or stochastic?)

SIR model as cellular automaton

Grid and states:

Each position on the grid is an individual
Three states: susceptible, infected, resistant

Rules:

A susceptible individual becomes infected with a probability depending on #infected neighbors (like before)
An infected individual can spontaneously be cured and become resistant. The probability that this happens is a fixed chance p_cure (also called recovery rate).

Exercises (optional)

You can do these at home to check your understanding, but they are optional and only for self-study.

Try it yourself
Go to computational-immunology.org/sir/, and use the SIR model simulator to answer the questions in the exercise sheet (see Brightspace).

The game of life

In Conway's "game of life", pixels on a grid follow 4 simple rules:

Black pixels with 0-1 black neighbors: black $\rightarrow$ white
Black pixels with 4-8 black neighbors: black $\rightarrow$ white
White pixels with 3 black neighbors: white $\rightarrow$ black
All other pixels stay the same color

Example:

Neighbors:

Result:

Question
Is this model deterministic or stochastic?

The game of life

Exercise (5 min)
What will the three grids below look like after one step? Rules: Black pixels with 0-1 black neighbors: black $\rightarrow$ white Black pixels with 4-8 black neighbors: black $\rightarrow$ white White pixels with 3 black neighbors: white $\rightarrow$ black All other pixels stay the same color

Simple rules, simple behavior?

The rules are pretty simple, so can we predict what will happen in the long run?

Discuss
What will be the end result if we play the game of life long enough? Will we have only black, only white, or both black and white pixels? Will there even be an "end result", or will the grid keep changing?

Simple rules, simple behavior?

The same rules can yield very different behavior depending on initial setup:

Static		Oscillating		Migrating

Simple rules, simple behavior?

The end result can be pretty complex...

Key Point
Even with simple rules, it can be hard to predict what happens over time!

Exercises

Again, these are only for self-study purposes:

Try it yourself
Go to https://bitstorm.org/gameoflife/, and use the game of life-simulator to answer the questions in the exercise sheet (see Brightspace).

Spatial patterns in biology

Alan Turing

Mathematician, computer scientist
Invented some of the fundamental concepts of computer science, including the idea of a "programmable computer"
Famous for cracking the enigma code during WWII
Also the founding father of theoretical biology!


Alan Turing (1912-1954)	Movie (2014)

Turing patterns

Turing wondered how symmetry breaking can occur in an organism (morphogenesis). He predicted that a reaction-diffusion system could do the trick if:

Reaction R produces molecules A and I
Molecule A activates reaction R
Molecule I inhibits reaction R
Molecule I diffuses much faster than A

These reactions exist: Belousov-Zhabotinsky reaction

Turing patterns

Turing himself had to do all computations by hand, but computing made things easier. This allows simulation of "real" patterns found in nature!

The Gray-Scott model

Another diffusion-reaction model that produces patterns: the Gray-Scott model

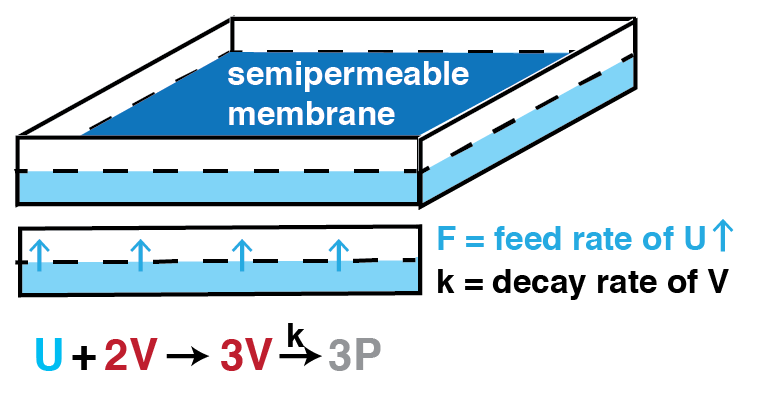
Molecule U reacts into molecule V
Reaction is catalyzed by 2 molecules of V
V decays into a waste product P at rate $k$
New U is supplied through a semi-permeable membrane at rate $F$
Both U and V can diffuse

The Gray-Scott model as a cellular automaton

The grid:

We now need 2 grids instead of 1 (1 for U, 1 for V)

The states:

We have not just a few states, but many (representing the amount of V and U)

The Gray-Scott model as a cellular automaton

So what about the rules? They should represent several processes:

New supply of U
Diffusion
Reaction of U to V
Decay of V

Exercise (5 min)
For each of the processes above, consider a position (pixel) p on the grid. On which grid(s) should the value G(p) at position p be updated (U, V, or both)? Which information (in the current grid of U, V, or both) should we use to determine what the updated value G*(p) should be?

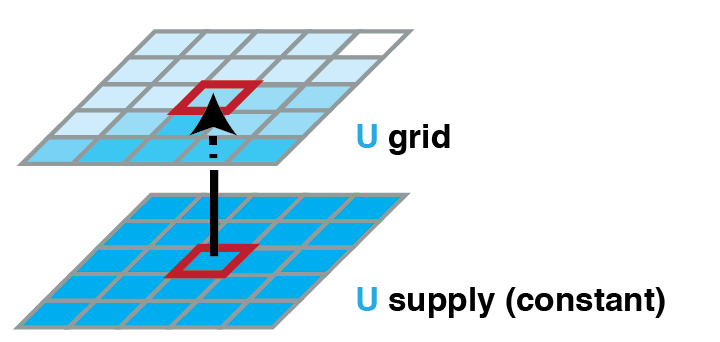
Worked example: Supply of U

Supply of U:

New U is supplied by diffusion through the membrane
What info do we need? We're talking diffusion of U. V probably doesn't change that. So we don't need V(p).
But the diffusion is going to depend on how much U_supply(p) and U(p) there is, so we do need U(p)
Do we need other info on U? From other p? Probably not.
So for example, we might say: U*(p) $\sim$ average of U(p) and U_supply

The Gray-Scott model as a cellular automaton

So what about the rules? They should represent several processes:

New supply of U
Diffusion
Reaction of U to V
Decay of V

Exercise (5 min)
For each of the processes above, consider a position (pixel) p on the grid. On which grid(s) should the value G(p) at position p be updated (U, V, or both)? Which information (in the current grid of U, V, or both) should we use to determine what the updated value G*(p) should be?

The Gray-Scott model as a cellular automaton

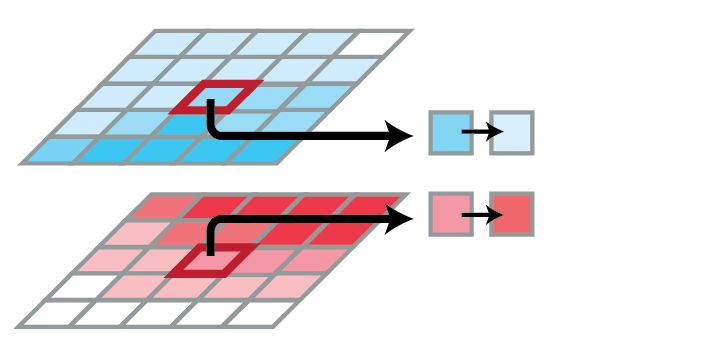
Diffusion:

Molecules diffuse independently of each other (U $\rightarrow$ U* and V $\rightarrow$ V*)
G*(p) depends on G(p), but also on G(neighbors of p)
G*(p) $\sim$ average of G(p_i), for p_i = p and all its neighbors in current grid

Supply of U:

New U is supplied by diffusion through a semi-permeable membrane!
U*(p) $\sim$ average of U(p) and U_supply

The Gray-Scott model as a cellular automaton

Reaction U $\rightarrow$ V:

Depends on amount U(p) and amount V(p) at p
A percentage x of U(p) reacts. This percentage depends on V(p).
U*(p) = U(p) - x,
V*(p) = V(p) + x

Decay of V:

Depends only on the current amount of V
New value at p = percentage of current value

The Gray-Scott model: predictions

Different patterns are possible in this model:

Exercises

Try it yourself
Go to https://mrob.com/pub/comp/xmorphia/ogl/index.html, and use the Gray-Scott simulator to answer the questions in the exercise sheet (see Brightspace).

Back to: why model complex systems like the TME?

Given some known "rules", eg:

if cells x and y interact, z happens
cell x moves towards cell y

We hope to understand/predict what is going on, eg:

tumor killed if we have more cell x

Discussion
We have seen that a combination of simple rules can already yield complex behavior, so that it is not always intuitive to predict what will happen over time. What do you think that means for research into the TME?

Summary

Cellular automata:

We can build a cellular automaton by defining a grid, the possible states, and some rules to determine what the next state will be
Rules can be deterministic or stochastic
They can depend only on one position p, or also on its neighbors
We can have multiple grids that communicate with each other

Next week: discuss even more complex models to simulate migrating cells